Apa itu Stack?
Stack merupakan struktur data yang digunakan dalam pemrograman untuk menyimpan data dalam urutan tertentu. Data yang dimasukkan terakhir akan dikeluarkan terlebih dahulu atau yang biasa disebut dengan LIFO (Last In First Out). Stack biasanya digunakan dalam pemanggilan fungsi, pengelolaan memori, dan pengolahan ekspresi matematika.
Operasi Stack Sederhana:
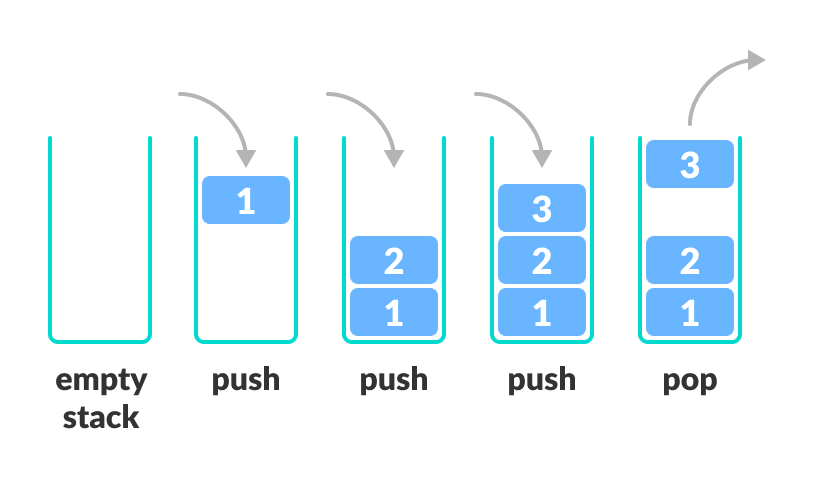
- Push (Menyisipkan Elemen):
- Operasi push digunakan untuk menambahkan elemen ke dalam tumpukan.
- Elemen ditambahkan ke bagian atas tumpukan.
- Pop (Menghapus Elemen):
- Operasi pop digunakan untuk menghapus elemen dari bagian atas tumpukan.
- Elemen yang dihapus adalah elemen terakhir yang ditambahkan ke dalam tumpukan.
- Peek (Melihat Elemen Teratas):
- Operasi peek digunakan untuk melihat elemen teratas tumpukan tanpa menghapusnya.
- Ini hanya mengembalikan nilai elemen teratas tanpa mengubah tumpukan.
- Is Empty (Memeriksa Keadaan Tumpukan):
- Operasi ini digunakan untuk memeriksa apakah tumpukan kosong.
- Mengembalikan true jika tumpukan kosong, dan false jika tidak.
Ekspresi Infix, Prefix, dan Postfix:
Ekspresi infix, prefix, dan postfix merujuk pada notasi yang digunakan dalam penulisan ekspresi matematika. Infix adalah bentuk umum yang umumnya ditemui dalam kehidupan sehari-hari, sedangkan prefix dan postfix merupakan notasi alternatif yang dikenal karena kemampuannya memudahkan proses perhitungan oleh komputer. Berikut adalah penjelasan rinci mengenai masing-masing notasi:
1. Infix:
- Infix adalah bentuk umum dari ekspresi matematika yang ditemui dalam literatur dan penggunaan sehari-hari.
- Operator ditempatkan di antara dua operand.
- Contoh: `a + b * c`
2. Prefix (Notasi Polandia):
- Dalam notasi ini, operator ditempatkan sebelum operand.
- Evaluasi ekspresi dilakukan dari kiri ke kanan.
- Contoh: `+ a * b c`
- Proses konversi dari infix ke prefix melibatkan pembalikan ekspresi infix dan penggantian operator.
3. Postfix (Notasi Reverse Polandia):
- Dalam notasi ini, operator ditempatkan setelah operand.
- Evaluasi ekspresi dilakukan dari kiri ke kanan.
- Contoh: `a b c * +`
- Proses konversi dari infix ke postfix juga melibatkan penggantian operator setelah pembalikan ekspresi infix.
- Contoh Konversi Infix ke Prefix dan Postfix:
Misalnya kita memiliki ekspresi infix: `A + B * C`
Konversi ke Prefix:
1. Melakukan pembalikan pada ekspresi infix: `C * B + A`
2. Menggantikan operator:
- `*` menjadi `* B C`
- `+` menjadi `+ * B C A`
3. Hasilnya: `+ * B C A`
Konversi ke Postfix:
1. Menggantikan operator:
- `+` menjadi `A B C * +`
2. Hasilnya: `A B C * +`
- Evaluasi Ekspresi Prefix dan Postfix:
Evaluasi Ekspresi Prefix:
- Membaca ekspresi dari kiri ke kanan.
- Saat menemukan operand, dimasukkan ke dalam stack.
- Saat menemukan operator, dua operand puncak stack di-pop, dioperasikan, dan hasilnya dimasukkan kembali ke dalam stack.
- Hasil akhir terletak di puncak stack.
Evaluasi Ekspresi Postfix:
- Membaca ekspresi dari kiri ke kanan.
- Saat menemukan operand, dimasukkan ke dalam stack.
- Saat menemukan operator, dua operand puncak stack di-pop, dioperasikan, dan hasilnya dimasukkan kembali ke dalam stack.
- Hasil akhir terletak di puncak stack.
Contoh Evaluasi Ekspresi Prefix: `+ * 3 4 5`
1. `* 3 4` = 12
2. `+ 12 5` = 17
Contoh Evaluasi Ekspresi Postfix: `3 4 * 5 +`
1. `3 4 *` = 12
2. `12 5 +` = 17




Komentar
Posting Komentar