Apa itu Graf dalam struktur data?
Struktur data graf merupakan kumpulan simpul yang memiliki data dan terhubung dengan simpul lainnya.
Mari kita coba memahaminya melalui contoh. Di Facebook, segalanya adalah simpul. Termasuk Pengguna, Foto, Album, Acara, Grup, Halaman, Komentar, Cerita, Video, Tautan, Catatan... apa pun yang memiliki data adalah simpul.
Setiap hubungan adalah tepian dari satu simpul ke simpul lainnya. Apakah Anda memposting foto, bergabung dengan grup, menyukai halaman, dll., tepian baru dibuat untuk hubungan tersebut.
 |
| Contoh Graf dalam Struktur Data |
Seluruh Facebook adalah kumpulan simpul dan tepian ini. Ini karena Facebook menggunakan struktur data graf untuk menyimpan datanya.
Secara lebih tepat, graf adalah struktur data (V, E) yang terdiri dari
1. Kumpulan simpul V
2. Kumpulan tepian E, direpresentasikan sebagai pasangan terurut dari simpul (u,v)
 |
| Simpul dan Tepian |
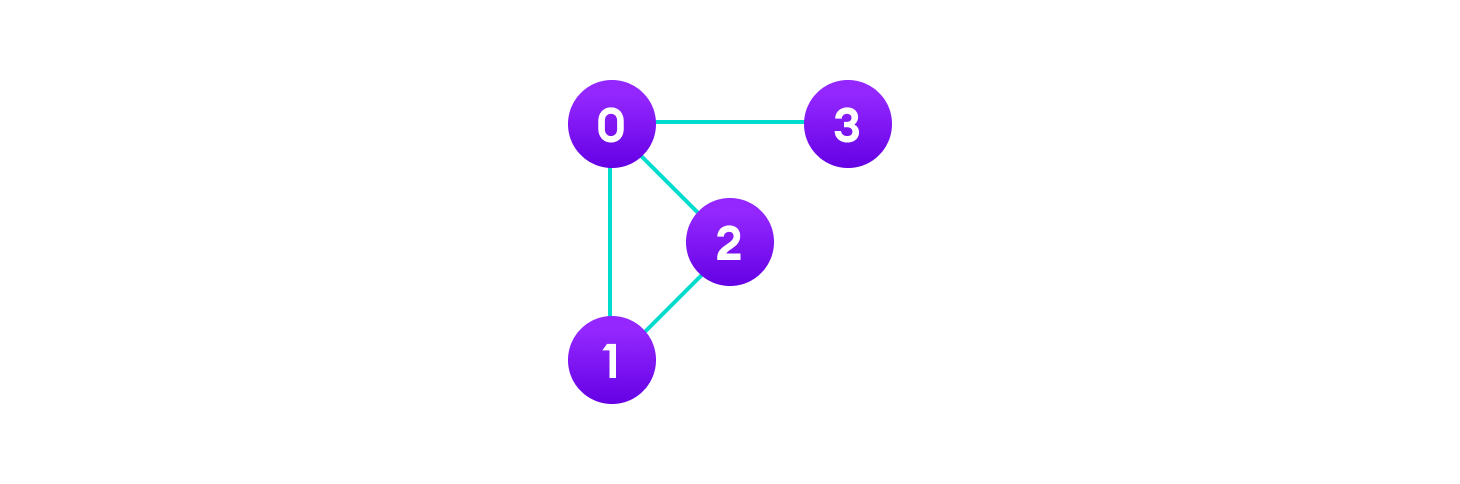
V = {0, 1, 2, 3}
E = {(0,1), (0,2), (0,3), (1,2)}
G = {V, E}
Terminologi Graf
- Adjacent: Sebuah simpul dikatakan berdekatan dengan simpul lain jika ada tepian yang menghubungkannya. Simpul 2 dan 3 tidak berdekatan karena tidak ada tepian di antara mereka.
- Path: Urutan tepian yang memungkinkan Anda pergi dari simpul A ke simpul B disebut jalur. 0-1, 1-2, dan 0-2 adalah jalur dari simpul 0 ke simpul 2.
- Drirected Graf: Graf di mana tepian (u,v) tidak selalu berarti bahwa ada tepian (v, u) juga. Tepian dalam graf seperti ini direpresentasikan oleh panah untuk menunjukkan arah tepian.
Representasi Graf
Graf biasanya direpresentasikan dalam dua cara:
1. Matriks adjacent
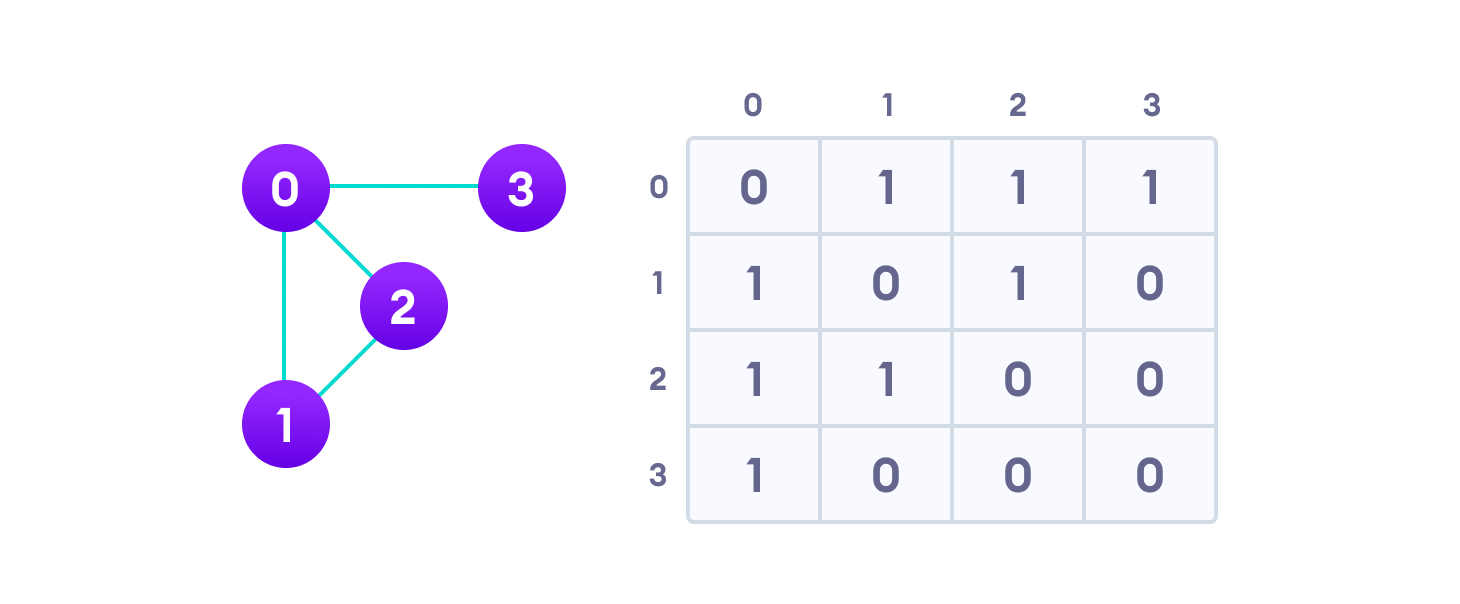
Matriks adjacent adalah larik 2D dari simpul V x V. Setiap baris dan kolom mewakili sebuah simpul.
Jika nilai elemen a[i][j] adalah 1, itu menunjukkan bahwa ada tepian yang menghubungkan simpul i dan simpul j.
Matriks adjacent untuk graf yang telah kita buat di atas adalah:
 |
| Matriks Adjacent |
Karena ini adalah graf tidak terarah, untuk tepian (0,2), kita juga perlu menandai tepian (2,0); membuat matriks adjacent simetris seputar diagonal.
Pencarian tepian (memeriksa apakah ada tepian antara simpul A dan simpul B) sangat cepat dalam representasi matriks adjacent tetapi kita harus menyediakan ruang untuk setiap kemungkinan hubungan antara semua simpul (V x V), sehingga membutuhkan lebih banyak ruang.
2. Adjacency list
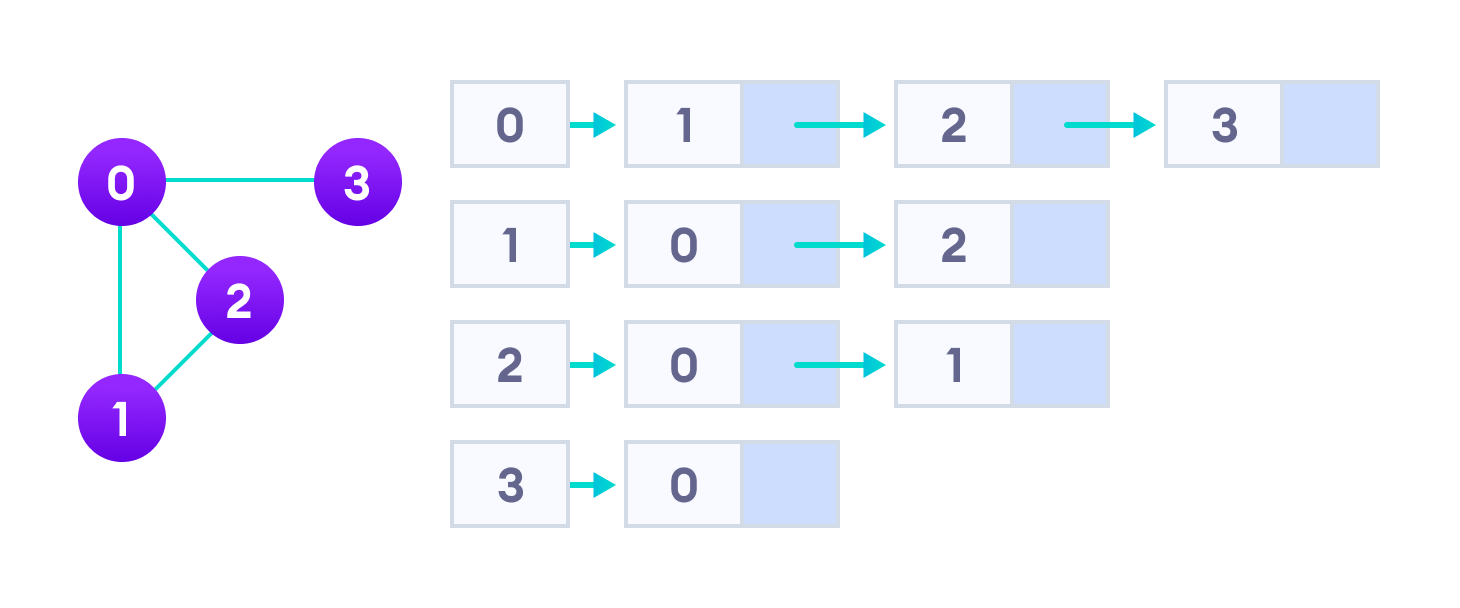
Adjacency list merepresentasikan graf sebagai larik dari daftar terkait.
Indeks larik mewakili sebuah simpul dan setiap elemen dalam daftar terkaitnya mewakili simpul lain yang membentuk tepian dengan simpul tersebut.
Adjacency list untuk graf yang kita buat dalam contoh pertama adalah sebagai berikut:
 |
| Representasi Adjacency list |
Adjacency list efisien dalam hal penyimpanan karena kita hanya perlu menyimpan nilai untuk tepian. Untuk graf dengan jutaan simpul, ini dapat berarti banyak ruang yang disimpan.
Operasi Graf
Operasi graf paling umum melibatkan:
- Memeriksa apakah elemen hadir dalam graf
- Traversal Graf
- Menambahkan elemen (simpul, tepian) ke graf
- Menemukan jalur dari satu simpul ke simpul lain
Komentar
Posting Komentar